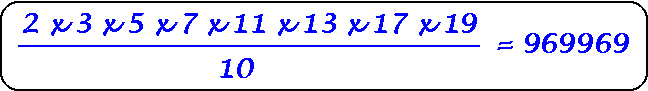This palindromic prime number reads the same upside down or when viewed in a mirror.
CONTENTS
Primes From Factorials !
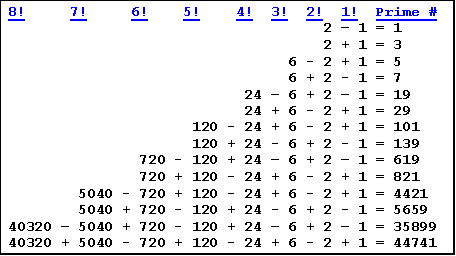
Factorial n (n!) means 1 x 2 x 3 x … x n
Unfortunately the next factorial results in a composite number.
The above shows the number 1 as a prime, although it is normally considered neither prime nor composite.
.
![]()
PRIME is Prime
Assign the value 1 to A, 2 to B, 3 to C, . . . , 26 to Z. Then
![]() i.e. 16 + 18 + 9 + 13
+ 5 = 61
i.e. 16 + 18 + 9 + 13
+ 5 = 61
![]()
Sum of 5 & 7 Consecutive Primes = a prime
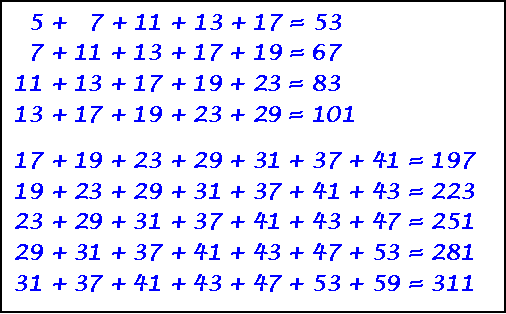
![]()

Above is shown three of the five series that use 2, the only even prime number.
Then I show one of each odd series from three to twenty-one. There are a total of sixty-one series with an odd number of primes (using primes < 100). every prime < 89 is the leading term in at least one series.
Charles w. Trigg, JRM 18(4),1985-86, p.247-248
![]()
5, 7 and 9 Digit Consecutive Primes
Three consecutive primes sum to a palindromic prime.
Visit Patrick De Geest's very attractive and informative WWW site about
Palindromic Numbers at Other
Links
The 9-digit set was reported by Jud McCranie
July 11, 1998
![]()
21 Consecutive Primes
The 21 consecutive primes from 7 to 89 sum to the prime number 953. Also when arranged in groups of three, each group sums to a prime. Furthermore, the reverse of these prime sums also sum to 953 !
T.V.Padmakrumar, JRM 27:1, 1995, p57
![]()
Near Repdigit Primes

All primes!
The next prime number in this series, though, is 17 threes
with a one at the end.
Some other numbers in this series (with less then 1800
threes) are:
3391 (that's 39 threes with a one at the
end
37831
317311
Near Repdigit Primes consist of
a series of the same digit, then one different digit; or one digit and then a
series of a different digit.
The above series is particularly attractive
because the number of threes in the first seven primes increase by one. There
are only eleven other primes in this series with less then 1800 threes.
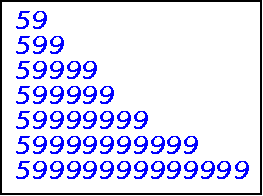 This is an example
of the other type of Near Repdigit Primes.
This is an example
of the other type of Near Repdigit Primes.
Some other numbers in this series
(with less then 4471 nines)
are:
5922
59361
594332
This last number is a prime consisting of a five followed by 4,332
nines!
There are many combinations of digits that make up Near Repdigit
Primes but the last digit in the number must be a 1, 3, 7, or 9.
![]()
Smallest and Largest Primes

of digit length from 1 to 15
![]()
5 & 71

The above two primes evenly divide the sum of the primes less then
themselves.
The only other such prime less then 2,000,000 is 369119, the
1577th prime.
D. Wells, Curious & Interesting Numbers
P.129
![]()
Fortunate Primes
Starting with 2 , find product of consecutive primes. Call it p
Then p + 1 = s
Take next largest prime >
s. Call it v. Then
v – p = prime.
Martin Gardner (The Last Recreations) calls these last numbers
‘fortunate primes’.

![]()
Primes in First k Digits of p

For k = 1,2,6, & 38. The next prime has at least 500 digits !
![]()
Palindromic Primes

11 is the only Palindromic prime with an even number of digits.
These are
the smallest and largest Palindromic primes of length 1 to 19.
Number of
palindromic primes of length 1=4, 2=1, 3=15, 5=93, 7=668, 9=5172
From PALPRI..HTM by Patrick De Geese, Belguim, July/96
Four Palindromic Primes

FromPALPRI..HTMbyPatrickDeGeese,Belguim,July/96
Link
to his page from Other
Links
Product of the first seven primes divided by ten gives a palindrome number.
9-Digit Palindromic Primes

| Palindromic Primes | There are a total of 5172 nine digit primes that read the same forward or backward. Many of them have extra properties. |
| Plateau Primes | There are 3 primes where all the interior digits are alike and are higher then the terminal digits. There are two primes, 322222223 & 722222227 in which the interior digits are smaller then the end ones. These are called Depression Primes |
| Undulating Primes | So called when adjacent digits are alternately greater or less then their neighbors. If there are only two distinct digits, they are called smoothly undulating. Of the total of 1006 undulating nine digit palindromic primes, seven are smoothly undulating. |
| Peak & Valley Primes | If the digits of the prime, reading left to right, steadily increase to a maximum value, and then steadily decrease, they are called peak primes. Valley primes are just the opposite. There are a total of 10 peak and 20 valley primes. 345676543 is unique because of the five consecutive digits. |
Depression Primes
 The above numbers
are called depression primes. The next ones in the 'two' series contain 27 and
63 two's! Note the 'seven 'two's in the one above. The next ones in the 'five'
series contain 19, 21, 57, 73 & 81 fives.
The above numbers
are called depression primes. The next ones in the 'two' series contain 27 and
63 two's! Note the 'seven 'two's in the one above. The next ones in the 'five'
series contain 19, 21, 57, 73 & 81 fives.
![]()
A Pandigital Palindromic Prime
 This 19
digit number reads the same forwards and backwards. It contains each of the
digits 0 to 9 twice, except the 7 which appears only once .
This 19
digit number reads the same forwards and backwards. It contains each of the
digits 0 to 9 twice, except the 7 which appears only once .
![]()
Ascending Pandigital Prime

This prime contains all the digits from 1 to 9 in order, then repeats
starting from 0.
Two similar primes but using only the nine digits from 1 to
9 are 1234567891 and 1234567891234567891234567891.
David Wells,
Curious & Interesting Numbers, p191

These numbers are all
primes!!
3911, it's reverse, and both numbers with a 3 on
either end or a 9 on either end.
There are a total of 102 reversible prime
pairs of four digits.
![]()
Reversable Primes

These primes are six digit reversable with an imbedded four digit reversable
prime.
For example, the top number of the middle column: following are all
prime; 311537, 335117, 735113, 711533, 1153, 3511..In this particular case,
31153, 71153 and 35117 are five digit primes, 11 and 53 are two digit primes,
and two 3’s, the 5 and the 7 are all one digit primes.
There are a total of
4769 reversible prime pairs of six digits.
Perfect Prime Squares

In each of these two squares, all rows, columns and the two main diagonals are distinct prime numbers when read in either direction. The order-5 square above is one of three reported by Mr. Card.
L. E. Card,Patterns in Primes, JRM 1:2, 1968, pp
.93-99, April 1968
![]()
 In 1998 Carlos B.
Rivera and Jaime Ayala rediscovered the order-4 shown above (L. E. Card) and
conjecture that it is the only solution with 20 distinct primes and no
palindromes. They also found another three order-5 Perfect Prime Squares with 24
distinct 5 digit primes (they call them Prime-magical squares). They also found
these two order-6 squares which each contain twenty-eight 6 digit primes.
In 1998 Carlos B.
Rivera and Jaime Ayala rediscovered the order-4 shown above (L. E. Card) and
conjecture that it is the only solution with 20 distinct primes and no
palindromes. They also found another three order-5 Perfect Prime Squares with 24
distinct 5 digit primes (they call them Prime-magical squares). They also found
these two order-6 squares which each contain twenty-eight 6 digit primes.
Carlos has a WWW page dealing with Prime Puzzles & Problems at http://www.sci.net.mx/~crivera/.
An Order-3 Superperfect Prime Square
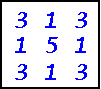 1 of the 24
possible order-3 perfect prime squares (not counting rotations and reflections.
Each row, column, and the two main diagonals all consist of 3-digit primes when
read in either direction. This one is superperfect because the partial
diagonal pairs are also prime numbers. The 5 can be replaced with an 8. It is
also Superperfect.
1 of the 24
possible order-3 perfect prime squares (not counting rotations and reflections.
Each row, column, and the two main diagonals all consist of 3-digit primes when
read in either direction. This one is superperfect because the partial
diagonal pairs are also prime numbers. The 5 can be replaced with an 8. It is
also Superperfect.
All order 2 and 3 perfect prime squares contain palindromes and contain duplicate prime numbers.
Do only Order-3 perfect prime squares contain palindromic primes? Are there any superperfect prime squares of order greater then 3?Charles W. Trigg,Perfect Prime Squares, JRM 17:2, 1984-85, pp .91-94, 1984-85
![]()
A Palindromic Sequence Series

Each sequence is formed from the one above it by inserting n, the row number, between all adjacent numbers that add to n. k is the number of numbers in each sequence. So far all k are prime numbers. Does this series continue indefinitely?
This pattern is credited to Leo Moser (Martin Gardner, The Last Recreations, p.199).
Digit Complementary Prime Pairs
A Diigit Complementary Prime Pair is defined as a pair of prime numbers in which digits in corresponding positions sum to 10 (or 0). There are 136 four digit pairs.
a.
a reversible prime pair b. the two primes contain 8 different digitsc. twin primes d. both primes contain consecutive digits
e. first member of the pair contains the 4 prime digits in order
f. each prime contains 3 digits the same
Charles W. Trigg, JRM 22:2, 1990, p 95-97
![]()
A Prime Circle

This is an example of a prime circle. Two adjacent numbers, including the last number and the first number, sum to a prime. In this particular case all the numbers are 3 digits. This circle is of length ninety, and is part of a 200 length prime circle found by Charles Ashbacher, JRM 26:1, 1994, p 63.
![]()
A String of Primes
 Start at the first
digit, or the first digit after any comma, and read a nine digit prime
number.
Start at the first
digit, or the first digit after any comma, and read a nine digit prime
number.
Three digits-all prime
 The only 3-digit
numbers such that all arrangements of their three digits are prime numbers.
The only 3-digit
numbers such that all arrangements of their three digits are prime numbers.
Also for 113, all 2-digit combinations are prime numbers.
![]()
Prime Factors of 114985
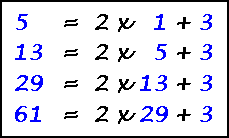
The prime factors of 114985 are 1, 5, 13, 29, 61.
![]()
Prime PPDI’s

The above three numbers are all Pluperfect Digital Invariants, meaning that when each digit of the number is raised to the power equal to the length of the number, the sum of these powers is equal to the original number.
i.e. 28116440335967 = 214 + 814 + 114 + 114 + 614 + 414 + 414 + 014 + 314 + 314 + 514 + 914 + 614 + 714.
The above three numbers are also PRIME !
They
are the only primes among the 79 PPDI’s under length forty.
The first number (the smallest) is the only one of the three that is pandigital. Also, of the four digits that appear twice,
three appear as adjacent pairs.
The largest number contains three digits that
appear four times and three digits that appear three times.
See Deimel & Jones, JRM 14(2), 1982, pp. 87 to 99 for list of the 79 PPDI’S to order 39.
Consecutive gaps between primes

![]()
Two Prime Pyramids
 All the numbers in
these pyramids are primes.
All the numbers in
these pyramids are primes.
Also...
All the numbers in the
first pyramid are reversible primes. All numbers in the second pyramid except
the fourth and sixth ones (8 & 12 digits) are also reversible primes. (The
next number in each sequence is composite).
![]()
Overlapping Primes

The largest known prime number such that any two adjacent digits are prime and all these primes are different.
David Wells ,Curious and Interesting Number, p. 195
All Primes!
 |
These are the largest possible primes with this
property. The top number of the second column as shown on page 191 of the
credit is a typo, as the number shown is composite. In the third set, the
last digit of the first number could be a three, as that number is also a
prime. The number ‘1’ here is presumed to be prime, although by definition
it is not.
Four other numbers with this property are 233399339, 29399999, 37337999 & 59393339 Chris K. Caldwell, Journal of Recreational Mathematics, 19:1, 1987,pp 30-33 David Wells, Curious & Interesting Numbers pps 191, 192, 200 |
 |
First and Last Columns are Prime Numbers
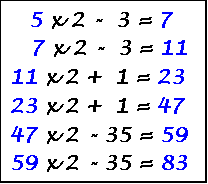
![]()
The First 7 Primes

Unfortunately, these relationships do not hold for the next higher prime, 19.
![]()
A Prime Series
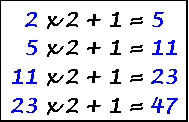
(Term n = Term n-1 times 2 plus 1)
Digital sums of prime pair products
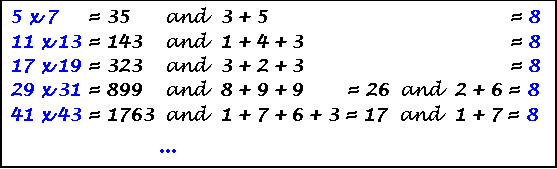
![]()
12-Digit Near-Repunit Primes

These are all the 12-digit primes of this type.
There is 1 with 3 digits, 1 with 5 digits, 1 with 6 digits,
2 with 8
digits, and 1 with 9 digits.
Next size after 12 digits is 17 with 2 such prime numbers.
C. Caldwell & H.Dubner JRM 27:1, 1995, p 35
A Prime Pair (relatively small)
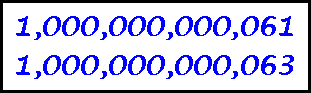 The two largest known
twin primes are 242206083 * 238880 . plus and minus 1 with 11713
digits, found by Indlekofer and Ja'rai in November, 1995. They are also the
first known gigantic twin primes (primes with at least 10,000 digits).
The two largest known
twin primes are 242206083 * 238880 . plus and minus 1 with 11713
digits, found by Indlekofer and Ja'rai in November, 1995. They are also the
first known gigantic twin primes (primes with at least 10,000 digits).
See http://www.utm.edu/research/primes/lists/top20/twin.html
![]()
Common Factors
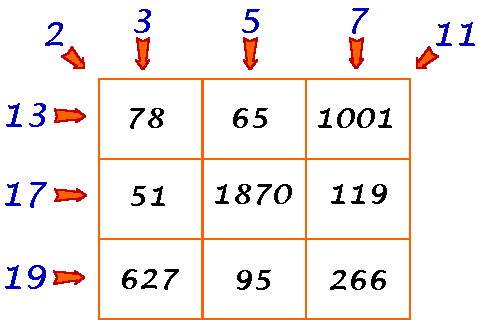
Each row, column and main diagonal has a common factor that is one of the first 8 prime numbers.
![]()
Palindrome Prime 373
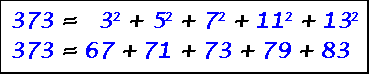
373 = sum of the squares of the first 5 odd primes
Also: the sum of five consecutive primes starting with 67.
From Patrick De Geest's Palindrome numbers WWW site at http://ping4.ping.be/~ping6758//index.shtml
![]()
Circular Primes

A circular prime is a prime number that remains prime as each leftmost digit
(msd)
in turn is moved to the right hand side.
From Patrick De Geest's Palindrome numbers WWW site (see above)
![]()
Priming the Cube
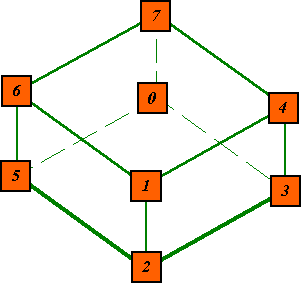
The only arrangement of 8 consecutive digits (not counting rotations or reflections) such that any two adjacent sum to a prime number.
![]()
Pairs equal Prime
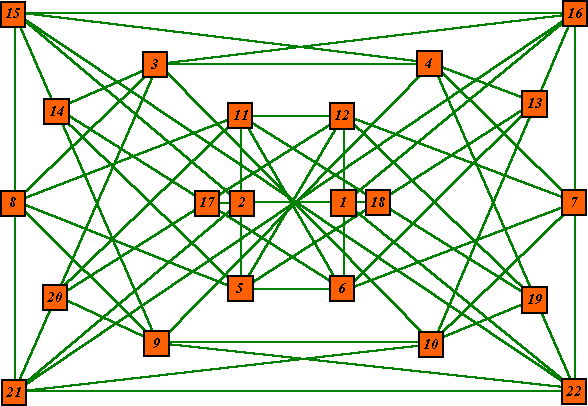
In this pattern the sum of each pair of numbers connected by a line sums to a
prime number.
The pattern is symmetrical both horizontally and vertically and
uses the consecutive numbers from 1 to 22.