A (normal) magic square consists of the distinct positive
integers 1, 2, ..., ![]() such that the sum of the
such that the sum of the ![]() numbers in any horizontal, vertical, or main diagonal line is
always the same magic
constant
numbers in any horizontal, vertical, or main diagonal line is
always the same magic
constant
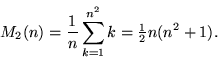
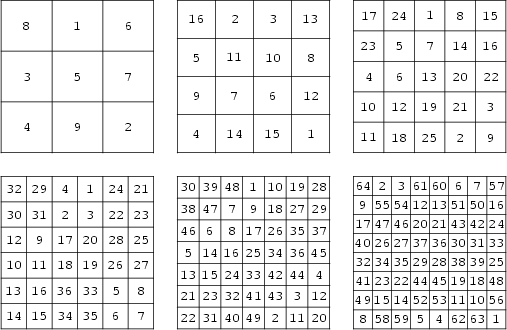
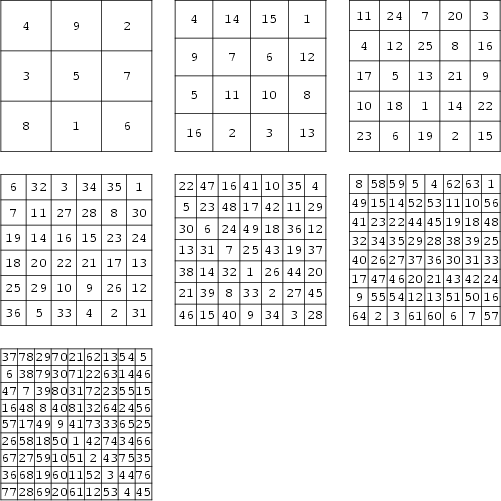
The unique normal square of order three was known to the ancient Chinese, who called it the Lo Shu. A version of the order 4 magic square with the numbers 15 and 14 in adjacent middle columns in the bottom row is called Dürer's magic square. Magic squares of order 3 through 8 are shown above.
The magic
constant for an ![]() th order magic square starting with an integer
th order magic square starting with an integer ![]() and with entries in an increasing arithmetic
series with difference
and with entries in an increasing arithmetic
series with difference ![]() between terms is
between terms is
(Hunter and Madachy 1975). If every number in a magic square is subtracted from
A square that fails to be magic only because one or both of the
main diagonal sums do not equal the magic
constant is called a semimagic
square. If all diagonals (including those obtained by
wrapping around) of a magic square sum to the magic
constant, the square is said to be a panmagic
square (also called a diabolic
square or pandiagonal
square). If replacing each number ![]() by its square
by its square ![]() produces another magic square, the
square is said to be a bimagic
square (or doubly
magic square). If a square is magic for
produces another magic square, the
square is said to be a bimagic
square (or doubly
magic square). If a square is magic for ![]() ,
, ![]() , and
, and ![]() , it is called a trebly
magic square. If all pairs of numbers symmetrically opposite the
center sum to
, it is called a trebly
magic square. If all pairs of numbers symmetrically opposite the
center sum to ![]() , the square is said to be an associative
magic square.
, the square is said to be an associative
magic square.

Kraitchik (1942) gives general techniques of constructing even and odd squares
of order ![]() . For
. For ![]() odd, a
very straightforward technique known as the Siamese method can be
used, as illustrated above (Kraitchik 1942, pp. 148-149). It
begins by placing a 1 in any location (in the center square of the
top row in the above example), then incrementally placing subsequent
numbers in the square one unit above and to the right. The counting
is wrapped around, so that falling off the top returns on the bottom
and falling off the right returns on the left. When a square is
encountered which is already filled, the next number is instead
placed below the previous one and the method continues as
before. The method, also called de la Loubere's method, is purported
to have been first reported in the West when de la Loubere returned
to France after serving as ambassador to Siam.
odd, a
very straightforward technique known as the Siamese method can be
used, as illustrated above (Kraitchik 1942, pp. 148-149). It
begins by placing a 1 in any location (in the center square of the
top row in the above example), then incrementally placing subsequent
numbers in the square one unit above and to the right. The counting
is wrapped around, so that falling off the top returns on the bottom
and falling off the right returns on the left. When a square is
encountered which is already filled, the next number is instead
placed below the previous one and the method continues as
before. The method, also called de la Loubere's method, is purported
to have been first reported in the West when de la Loubere returned
to France after serving as ambassador to Siam.
A generalization of this method uses an "ordinary vector" ![]() which gives the offset for each noncolliding move and a
"break vector"
which gives the offset for each noncolliding move and a
"break vector" ![]() which gives the offset to introduce
upon a collision. The standard Siamese method therefore has ordinary
vector (1,
which gives the offset to introduce
upon a collision. The standard Siamese method therefore has ordinary
vector (1, ![]() and break vector (0, 1). In order
for this to produce a magic square, each break move must end up on
an unfilled cell. Special classes of magic squares can be
constructed by considering the absolute sums
and break vector (0, 1). In order
for this to produce a magic square, each break move must end up on
an unfilled cell. Special classes of magic squares can be
constructed by considering the absolute sums ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Call the set of these numbers the
sumdiffs (sums and differences). If all sumdiffs are relatively
prime to
. Call the set of these numbers the
sumdiffs (sums and differences). If all sumdiffs are relatively
prime to ![]() and the square is a magic square,
then the square is also a panmagic
square. This theory originated with de la Hire. The following
table gives the sumdiffs for particular choices of ordinary and
break vectors.
and the square is a magic square,
then the square is also a panmagic
square. This theory originated with de la Hire. The following
table gives the sumdiffs for particular choices of ordinary and
break vectors.
| Ordinary Vector | Break Vector | Sumdiffs | Magic Squares | Panmagic Squares |
| (1, |
(0, 1) | (1, 3) | none | |
| (1, |
(0, 2) | (0, 2) | none | |
| (2, 1) | (1, |
(1, 2, 3, 4) | none | |
| (2, 1) | (1, |
(0, 1, 2, 3) | ||
| (2, 1) | (1, 0) | (0, 1, 2) | none | |
| (2, 1) | (1, 2) | (0, 1, 2, 3) | none |
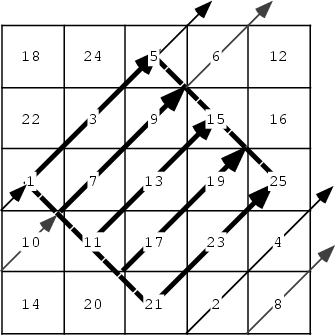
A second method for generating magic squares of odd order has been discussed by J. H. Conway under the name of the "lozenge" method. As illustrated above, in this method, the odd numbers are built up along diagonal lines in the shape of a diamond in the central part of the square. The even numbers which were missed are then added sequentially along the continuation of the diagonal obtained by wrapping around the square until the wrapped diagonal reaches its initial point. In the above square, the first diagonal therefore fills in 1, 3, 5, 2, 4, the second diagonal fills in 7, 9, 6, 8, 10, and so on.
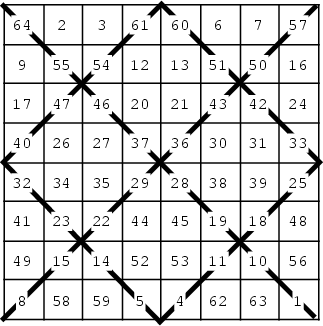
An elegant method for constructing magic squares of doubly
even order ![]() is to draw
is to draw ![]() s through each
s through each ![]() subsquare and fill all squares in sequence. Then replace each entry
subsquare and fill all squares in sequence. Then replace each entry
![]() on a crossed-off diagonal by
on a crossed-off diagonal by ![]() or, equivalently, reverse the order of the crossed-out
entries. Thus in the above example for
or, equivalently, reverse the order of the crossed-out
entries. Thus in the above example for ![]() , the crossed-out numbers are originally 1, 4, ..., 61, 64,
so entry 1 is replaced with 64, 4 with 61, etc.
, the crossed-out numbers are originally 1, 4, ..., 61, 64,
so entry 1 is replaced with 64, 4 with 61, etc.
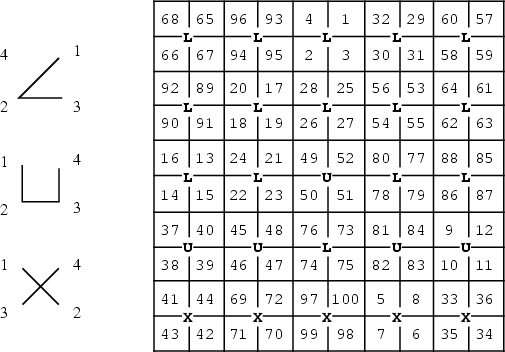
A very elegant method for constructing magic squares of singly
even order ![]() with
with ![]() (there is no magic square of order 2) is due to
J. H. Conway, who calls it the "LUX" method. Create an
array consisting of
(there is no magic square of order 2) is due to
J. H. Conway, who calls it the "LUX" method. Create an
array consisting of ![]() rows of
rows of ![]() s, 1 row of Us, and
s, 1 row of Us, and ![]() rows of
rows of ![]() s, all of length
s, all of length ![]() . Interchange the middle U with the L above it. Now
generate the magic square of order
. Interchange the middle U with the L above it. Now
generate the magic square of order ![]() using the Siamese method centered on the array of letters (starting
in the center square of the top row), but fill each set of four
squares surrounding a letter sequentially according to the order
prescribed by the letter. That order is illustrated on the left side
of the above figure, and the completed square is illustrated to the
right. The "shapes" of the letters L, U, and X naturally suggest the
filling order, hence the name of the algorithm.
using the Siamese method centered on the array of letters (starting
in the center square of the top row), but fill each set of four
squares surrounding a letter sequentially according to the order
prescribed by the letter. That order is illustrated on the left side
of the above figure, and the completed square is illustrated to the
right. The "shapes" of the letters L, U, and X naturally suggest the
filling order, hence the name of the algorithm.
It is an unsolved problem to determine the number of magic
squares of an arbitrary order, but the number of distinct magic
squares (excluding those obtained by rotation and reflection) of
order ![]() , 2, ... are 1, 0, 1, 880, 275305224, ...
(Sloane's A006052;
Madachy 1979, p. 87). The 880 squares of order four were
enumerated by Frenicle de Bessy in the seventeenth century, and are
illustrated in Berlekamp et al. (1982, pp. 778-783). The
number of
, 2, ... are 1, 0, 1, 880, 275305224, ...
(Sloane's A006052;
Madachy 1979, p. 87). The 880 squares of order four were
enumerated by Frenicle de Bessy in the seventeenth century, and are
illustrated in Berlekamp et al. (1982, pp. 778-783). The
number of ![]() squares is not known, but Pinn and
Wieczerkowski (1998) estimated it to be
squares is not known, but Pinn and
Wieczerkowski (1998) estimated it to be ![]() using Monte Carlo simulation and methods from statistical
mechanics.
using Monte Carlo simulation and methods from statistical
mechanics.
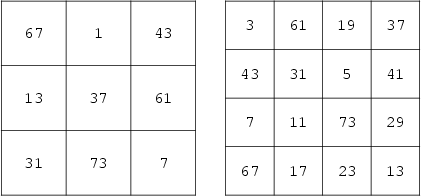
The above magic squares consist only of primes and were discovered by E. Dudeney (1970) and A. W. Johnson, Jr. (Gardner 1984, p. 86; Dewdney 1988). Madachy (1979, pp. 93-96) and Rivera discuss other magic squares composed of primes.

Benjamin Franklin constructed the above ![]() panmagic
square having magic
constant 260. Any half-row or half-column in this square totals
130, and the four corners plus the middle total 260. In addition,
bent diagonals (such as 52-3-5-54-10-57-63-16) also total 260
(Madachy 1979, p. 87).
panmagic
square having magic
constant 260. Any half-row or half-column in this square totals
130, and the four corners plus the middle total 260. In addition,
bent diagonals (such as 52-3-5-54-10-57-63-16) also total 260
(Madachy 1979, p. 87).
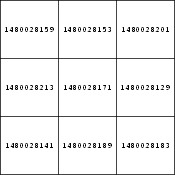
In addition to other special types of magic squares, a ![]() square whose entries are consecutive primes,
illustrated above, has been discovered by H. Nelson (Rivera).
square whose entries are consecutive primes,
illustrated above, has been discovered by H. Nelson (Rivera).
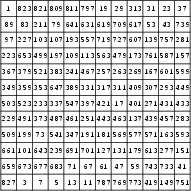
According to a 1913 proof of J. N. Murray (cited in Gardner 1984, pp. 86-87), the smallest magic square composed of consecutive primes starting with 3 and including the number 1 is of order 12.
Variations on magic squares can also be constructed using letters (either in defining the square or as entries in it), such as the alphamagic square and templar magic square.
Various numerological properties have also been associated with magic squares. Pivari associates the squares illustrated above with Saturn, Jupiter, Mars, the Sun, Venus, Mercury, and the Moon, respectively. Attractive patterns are obtained by connecting consecutive numbers in each of the squares (with the exception of the Sun magic square).